Android上实现水波特效
罗朝辉(http://www.cppblog.com/kesalin)
转载请注明出处
说明:
本文水波算法部分整理自GameRes上的资料,原作者Imagic。我只是在学习Android的过程中,想到这个特效,然后就在Android上实现出来,并在源算法的基础上添加了雨滴滴落特效,以及划过水面时的涟漪特效。 该程序在模拟器和真机上运行速度都较慢,需要进一步优化或使用JNI实现,如果你想到好的优化算法,请联系我:kesalin@gmail.com。
示例程序下载:http://www.cppblog.com/Files/kesalin/RippleDemo.zip
本文pdf文档下载:点击这里
基础知识:
在讲解代码之前,我们来回顾一下在高中的物理课上我们所学的关于水波的知识。水波有扩散,衰减,折射,反射,衍射等几个特性:
扩散:当你投一块石头到水中,你会看到一个以石头入水点为圆心所形成的一圈圈的水波,这里,你可能会被这个现象所误导,以为水波上的每一点都是以石头入水点为中心向外扩散的,这是错误的。实际上,水波上的任何一点在任何时候都是以自己为圆心向四周扩散的,之所以会形成一个环状的水波,是因为水波的内部因为扩散的对称而相互抵消了。
衰减:因为水是有阻尼的,否则,当你在水池中投入石头,水波就会永不停止的震荡下去。
折射:因为水波上不同地点的倾斜角度不同,所以我们从观察点垂直往下看到的水底并不是在观察点的正下方,而有一定的偏移。如果不考虑水面上部的光线反射,这就是我们能感觉到水波形状的原因。
反射:水波遇到障碍物会反射。
衍射:在水池中央放上一块礁石,或放一个中间有缝的隔板,那么就能看到水波的衍射现象了。
算法推导:
好了,有了这几个特性,再运用数学和几何知识,我们就可以模拟出真实的水波了。但是,如果你曾用3DMax做过水波的动画,你就会知道要渲染出一幅真实形状的水波画面少说也得好几十秒,而我们现在需要的是实时的渲染,每秒种至少也得渲染20帧才能使得水波得以平滑的显示。考虑到电脑运算的速度,我们不可能按照正弦函数或精确的公式来构造水波,不能用乘除法,更不能用sin、cos等三角函数,只能用一种取近似值的快速算法,尽管这种算法存在一定误差,但是为了满足实时动画的要求,我们不得不这样做。
首先我们要建立两个与水池图象一样大小的数组buf1[PoolWidth * PoolHeight]和buf2[PoolWidth * PoolHeight](PoolWidth为水池图象的象素宽度、PoolHeight为水池图象的象素高度),用来保存水面上每一个点的前一时刻和后一时刻波幅数据,因为波幅也就代表了波的能量,所以在后面我们称这两个数组为波能缓冲区。水面在初始状态时是一个平面,各点的波幅都为0,所以,这两个数组的初始值都等于0。
下面来推导计算波幅的公式
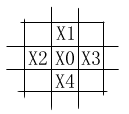
我们假设存在这样一个一次公式,可以在任意时刻根据某一个点周围前、后、左、右四个点以及该点自身的振幅来推算出下一时刻该点的振幅,那么,我们就有可能用归纳法求出任意时刻这个水面上任意一点的振幅。如左图,你可以看到,某一时刻,X0点的振幅除了受X0点自身振幅的影响外,同时受来自它周围前、后、左、右四个点(X1、X2、X3、X4)的影响(为了简化,我们忽略了其它所有点),而且,这四个点对X0点的影响力可以说是机会均等的。那么我们可以假设这个一次公式为:
|
X0’= a * (X1 + X2 + X3 + X4) + b * X0 (公式1)
|
a, b为待定系数,X0’为X0点下一时刻的振幅,
X0、X1、X2、X3、X4为当前时刻的振幅
下面我们来求解a和b。
假设水的阻尼为0。在这种理想条件下,水的总势能将保持不变,水波永远波动。也就是说在任何时刻,所有点的振幅的和保持不变。那么可以得到下面这个公式:
|
X0’+ X1’+ ... + Xn’ = X0 + X1 + ... + Xn
|
将每一个点用公式1替代,代入上式,得到:
|
(4a+ b) * X0 + (4a+ b) * X1 + ... (4a+ b) * Xn = X0 + X1 + ... + Xn=>4a+ b = 1
|
找出一个最简解:a = 1/2、b = -1。
因为1/2可以用移位运算符“>>”来进行,不用进行乘除法,所以,这组解是最适用的而且是最快的。那么最后得到的公式就是:
|
X0’=(X1 + X2 + X3 + X4)/ 2 - X0
|
好了,有了上面这个近似公式,你就可以推广到下面这个一般结论:已知某一时刻水面上任意一点的波幅,那么,在下一时刻,任意一点的波幅就等于与该点紧邻的前、后、左、右四点的波幅的和除以2、再减去该点的波幅。
应该注意到,水在实际中是存在阻尼的,否则,用上面这个公式,一旦你在水中增加一个波源,水面将永不停止的震荡下去。所以,还需要对波幅数据进行衰减处理,让每一个点在经过一次计算后,波幅都比理想值按一定的比例降低。这个衰减率经过测试,用1/32比较合适,也就是1/2^5。可以通过移位运算很快的获得。
到这里,水波特效算法中最艰难的部分已经明了,下面是Android源程序中计算波幅数据的代码。
|
//某点下一时刻的波幅算法为:上下左右四点的波幅和的一半减去当前波幅,即
//X0' =(X1 + X2 + X3 + X4)/ 2 - X0
//+----x3----+
//+|+
//+|+
//x1---x0----x2
//+|+
//+|+
//+----x4----+
//
voidrippleSpread()
{
intpixels =m_width* (m_height- 1);
for(inti =m_width; i < pixels; ++i) {
//波能扩散:上下左右四点的波幅和的一半减去当前波幅
// X0' =(X1 + X2 + X3 + X4)/ 2 - X0
//
m_buf2[i] =
(short)(((m_buf1[i - 1] +m_buf1[i + 1]+
m_buf1[i -m_width] +m_buf1[i +m_width]) >> 1)
-m_buf2[i]);
//波能衰减1/32
//
m_buf2[i] -=m_buf2[i] >> 5;
}
//交换波能数据缓冲区
short[] temp =m_buf1;
m_buf1=m_buf2;
m_buf2= temp;
}
|
渲染:
然后我们可以根据算出的波幅数据对页面进行渲染。
因为水的折射,当水面不与我们的视线相垂直的时候,我们所看到的水下的景物并不是在观察点的正下方,而存在一定的偏移。偏移的程度与水波的斜率,水的折射率和水的深度都有关系,如果要进行精确的计算的话,显然是很不现实的。同样,我们只需要做线性的近似处理就行了。因为水面越倾斜,所看到的水下景物偏移量就越大,所以,我们可以近似的用水面上某点的前后、左右两点的波幅之差来代表所看到水底景物的偏移量。
在程序中,用一个页面装载原始的图像,用另外一个页面来进行渲染。先取得指向两个页面内存区的指针src和dst,然后用根据偏移量将原始图像上的每一个象素复制到渲染页面上。进行页面渲染的代码如下:
|
voidrippleRender()
{
intoffset;
inti =m_width;
intlength =m_width*m_height;
for(inty = 1; y <m_height- 1; ++y) {
for(intx = 0; x <m_width; ++x, ++i) {
//计算出偏移象素和原始象素的内存地址偏移量:
//offset = width *yoffset+xoffset
offset = (m_width* (m_buf1[i -m_width] -m_buf1[i +m_width])) + (m_buf1[i - 1] -m_buf1[i + 1]);
//判断坐标是否在范围内
if(i + offset > 0 && i + offset < length) {
m_bitmap2[i] =m_bitmap1[i + offset];
}
else{
m_bitmap2[i] =m_bitmap1[i];
}
}
}
}
|
增加波源:
俗话说:无风不起浪,为了形成水波,我们必须在水池中加入波源,你可以想象成向水中投入石头,形成的波源的大小和能量与石头的半径和你扔石头的力量都有关系。知道了这些,那么好,我们只要修改波能数据缓冲区buf,让它在石头入水的地点来一个负的“尖脉冲”,即让buf[x,y] = -n。经过实验,n的范围在(32 ~ 128)之间比较合适。
控制波源半径也好办,你只要以石头入水中心点为圆心,画一个以石头半径为半径的圆,让这个圆中所有的点都来这么一个负的“尖脉冲”就可以了(这里也做了近似处理)。
增加波源的代码如下:
|
// stoneSize:波源半径
// stoneWeight:波源能量
//
voiddropStone(intx,inty,intstoneSize,intstoneWeight)
{
//判断坐标是否在范围内
if((x + stoneSize) >m_width|| (y + stoneSize) >m_height
|| (x - stoneSize) < 0 || (y - stoneSize) < 0) {
return;
}
intvalue = stoneSize * stoneSize;
shortweight = (short)-stoneWeight;
for(intposx = x - stoneSize; posx < x + stoneSize; ++posx){
for(intposy = y - stoneSize; posy < y + stoneSize; ++posy){
if((posx - x) * (posx - x) + (posy - y) * (posy - y)
< value)
{
m_buf1[m_width* posy + posx] = weight;
}
}
}
}
|
如果我们想要模拟在水面划过时引起的涟漪效果,那么我们还需要增加新的算法函数breasenhamDrop。
|
voiddropStoneLine(intx,inty,intstoneSize,intstoneWeight) {
//判断坐标是否在屏幕范围内
if((x + stoneSize) >m_width|| (y + stoneSize) >m_height
|| (x - stoneSize) < 0 || (y - stoneSize) < 0) {
return;
}
for(intposx = x - stoneSize; posx < x + stoneSize; ++posx){
for(intposy = y - stoneSize; posy < y + stoneSize; ++posy){
m_buf1[m_width* posy + posx] = -40;
}
}
}
//xs,ys:起始点,xe,ye:终止点
// size :波源半径,weight :波源能量
voidbreasenhamDrop(intxs,intys,intxe,intye,intsize,intweight)
{
intdx = xe - xs;
intdy = ye - ys;
dx = (dx >= 0) ? dx : -dx;
dy = (dy >= 0) ? dy : -dy;
if(dx == 0 && dy == 0) {
dropStoneLine(xs, ys, size, weight);
}
elseif(dx == 0) {
intyinc = (ye - ys != 0) ? 1 : -1;
for(inti = 0; i < dy; ++i){
dropStoneLine(xs, ys, size, weight);
ys += yinc;
}
}
elseif(dy == 0) {
intxinc = (xe - xs != 0) ? 1 : -1;
for(inti = 0; i < dx; ++i){
dropStoneLine(xs, ys, size, weight);
xs += xinc;
}
}
elseif(dx > dy) {
intp = (dy << 1) - dx;
intinc1 = (dy << 1);
intinc2 = ((dy - dx) << 1);
intxinc = (xe - xs != 0) ? 1 : -1;
intyinc = (ye - ys != 0) ? 1 : -1;
for(inti = 0; i < dx; ++i) {
dropStoneLine(xs, ys, size, weight);
xs += xinc;
if(p < 0) {
p += inc1;
}
else{
ys += yinc;
p += inc2;
}
}
}
else{
intp = (dx << 1) - dy;
intinc1 = (dx << 1);
intinc2 = ((dx - dy) << 1);
intxinc = (xe - xs != 0) ? 1 : -1;
intyinc = (ye - ys != 0) ? 1 : -1;
for(inti = 0; i < dy; ++i) {
dropStoneLine(xs, ys, size, weight);
ys += yinc;
if(p < 0) {
p += inc1;
}
else{
xs += xinc;
p += inc2;
}
}
}
}
|
效果图:
|

划过水面时的涟漪特效
|

雨滴滴落水面特效
|
结语:
这种用数据缓冲区对图像进行水波处理的方法,有个最大的好处就是,程序运算和显示的速度与水波的复杂程度是没有关系的,无论水面是风平浪静还是波涛汹涌,程序的fps始终保持不变,这一点你研究一下程序就应该可以看出来。
分享到:











相关推荐
Android——实现光点模糊渐变的自旋转圆环特效,实现水滴波纹特效的源代码。 博客地址:http://blog.csdn.net/qq_22770457?viewmode=contents
Android——实现光点模糊渐变的自旋转圆环特效,实现水滴波纹特效
水波纹加载特效,贝塞尔曲线核心算法。
非常有意思的一个效果,适用于页面切换等特效
Android实现的雷达扫描和水波纹效果
主要为大家详细介绍了Android实现水波纹特效,具有一定的参考价值,感兴趣的小伙伴们可以参考一下
按钮特效
不多说直接上图 是不是很震撼.这个库的波纹算法是基于阿德里安波音公司的文章。国外大牛就是厉害。 下面贴出使用方法: 第一步:添加gradledependencies { compile 'com.github.r21nomi:glrippleview:1.0.0' ...
Android水波效果工程源码,实现了雨滴滴落特效,以及划过水面时的涟漪特效
Android动画特效之水波(地震波)报警动画,参考博文:http://blog.csdn.net/daijin888888/article/details/46357515
仿水波纹流球进度条控制器,Android实现高端大气的主流特效,供大家参考,具体内容如下 效果图: CircleView 这里主要是实现中心圆以及水波特效 package com.lgl.circleview; import android.content.Context; ...
水波纹,涟漪效果,可用于设备查找之类的特效
安卓源码包android 动画效果Android 烟花效果源码等21个合集...自定义视图实现水波从中心扩散效果.rar 超爽的android抽屉效果.rar 雪花飘落效果,代码很简单!!!!!.zip 高仿墨迹天气背景动画效果-云,风,雪等.rar
根据自己的博文写的一个Android水波纹过渡动画,相信你一定喜欢的,十分炫酷!
Ripple是一个类似雷达搜索引擎,波纹效果很好看,从studio改来的,...水波会慢慢泛开,可以自己设置波纹条数量,范围和颜色.zip,太多无法一一验证是否可用,程序如果跑不起来需要自调,部分代码功能进行参考学习。
Shape Ripple is a library that emulates a ripple like animations with cool tweaks on the go. It runs on API level 11 and upwards. As addition you can even create your own shape renderer through the ...
主要介绍了Android波纹扩散效果之仿支付宝咻一咻功能实现波纹扩散特效的相关资料,需要的朋友可以参考下
import android.support.v4.view.animation.LinearOutSlowInInterpolator; import android.support.v7.app.AppCompatActivity; import android.view.View; import android.widget.Button; public class MainActi
点击出现水波纹类似的特效,实现的逻辑也很简单,值得我们去学习